Resistencia de los materiales
RESISTENCIA DE LOS MATERIALES
• Tensión: Se denomina tensión a la fuerza que es ejercida mediante la acción de un cable, cuerda, cadena u otro objeto sólido similar.
• Tracción: Esfuerzo a que está sometido un cuerpo por la aplicación de dos fuerzas que actúan en sentido opuesto, y tienden a estirarlo, aumentando su longitud y disminuyendo su sección.
• Cortadura: Esfuerzo que tiende a cortar el objeto por la aplicación de dos fuerzas en sentidos contrarios y no alineadas.
• El esfuerzo de flexión: provoca tensiones de tracción y compresión, produciéndose las máximas en el cordón inferior y en el cordón superior respectivamente, las cuales se calculan relacionando el momento flector y el segundo momento de inercia.
Vigas hiperestáticas: Son aquellas vigas que, para su cálculo, presentan mas incógnitas que ecuaciones. En general, una estructura es hiperestática o estáticamente indeterminada cuando está en equilibrio pero las ecuaciones de la estática resultan insuficientes para determinar todas las fuerzas internas o las reacciones.
Las propiedades mecánicas de la materia son la elasticidad, la compresión y la tensión. Definimos a un cuerpo elástico, como aquel que recobra su tamaño y forma original cuando deja de actuar sobre él una fuerza deformante. Las bandas de hule, las pelotas de golf, los trampolines, las camas elásticas, las pelotas de fútbol y los resortes son ejemplos comunes de cuerpos elásticos. Para todos los cuerpos elásticos, conviene establecer relaciones de causa y efecto entre la deformación y las fuerzas deformantes.
La Ley de Hooke no se limita al caso de los resortes en espiral; de hecho, se aplica a la deformación de todos los cuerpos elásticos. Para que la Ley pueda aplicar de un modo más general, es conveniente definir los términos esfuerzo y deformación. El Esfuerzo se refiere a la causa de una deformación elástica, mientras que la deformación se refiere a su efecto, es decir a la deformación en sí misma. Existen 3 tipos de esfuerzos, los de tensión, de compresión y cortantes, en este subtema, nos centraremos a analizar el esfuerzo de tensión que se presenta cuando fuerzas iguales y opuestas se apartan entre sí.
La Ley de Hooke, establece:
Una columna es un elemento sometido a compresión, el cual es lo suficientemente delgado respecto a su longitud para que bajo la acción de una carga gradualmente creciente se rompa por flexión lateral o pandeo ante una carga mucho menor que la necesaria para romperlo por aplastamiento.
Contenido
1. Conceptos
2. Esfuerzo y deformación debido a cargas externas: esfuerzos mecánicos y térmicos y Ley de Hooke
3. Vigas con dos apoyos cargadas en puntos: vigas con cargas uniformes, vigas hiperestaticas y vigas en Cantiliver
4. Clasificación de columnas
5. Conclusiones y créditos
1. Conceptos
• Cuerpo elástico: Aquel que recobra su tamaño y forma original cuando deja de actuar sobre él una fuerza deformante. Las bandas de hule, las pelotas de golf, los trampolines, las camas elásticas, las pelotas de fútbol y los resortes son ejemplos comunes de cuerpos elásticos.
• Compresión: Consiste en someter a un cuerpo a la acción de dos fuerzas opuestas para que disminuya su volumen. Se conoce como esfuerzo de compresión al resultado de estas tensiones.
• Esfuerzo: Es la razón de una fuerza aplicada entre el área sobre el cual actúa, por ejemplo Newtons/m2 , o libras/ft2.
• El límite elástico: Es el esfuerzo máximo que puede sufrir un cuerpo sin que la deformación sea permanente.
• Viga: Se denomina viga a un elemento constructivo lineal que trabaja principalmente a flexión.
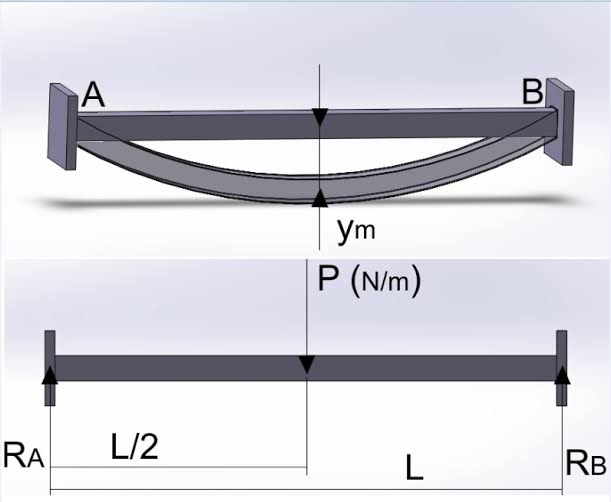
• Vigas con cargas uniformes: Considerando una porción de una viga sometida a una carga uniforme w, cada segmento dx de la carga w crea una fuerza concentrada igual a dF = wdx sobre la viga. Si dF está localizada en x, donde la ordenada de la línea de influencia de la viga para alguna función (reacción, cortante o momento) es y, entonces el valor de la función es (dF)(y) = (wdx)y.
• Vigas en Cantiliver: También se les llama vigas en voladizo. En estas vigas un extremo esta fijo para impedir la rotación; también se conoce como un extremo empotrado, debido a la clase de apoyo.
• Columna: Es un soporte vertical, de forma alargada, que permite sostener el peso de una estructura. Lo habitual es que su sección sea circular: cuando es cuadrangular, recibe el nombre de pilar.
• Columnas Largas: columna cuya capacidad de carga está limitada por el pandeo antes que por la resistencia.
• Columna estriada o acanalada: Aquella cuya forma posee estrías o acanaladuras ornamentales en toda su longitud.
• Columna fasciculada: La que está conformada por una serie de delgados fustes, similares, agrupados a modo de haz.
• Columna fajada o anillada: La que tiene su fuste despiezado en tambores, anillos o fajas de distinto diámetro.
• Columna geminada: La que tiene fuste doble.
• Falla en las columnas: La columna es un elemento estructural que trabaja en compresión, pero por su ubicación en el sistema estructural debe soportar también flexiones, corte y torsión.
• Relación de esbeltez de las columnas: Es una medida de la flexibilidad de la columna sirve para clasificar a las columnas en cortas, largas e intermedias. Depende de la relación entre la longitud y el diámetro de la columna, pero también de la relación de la longitud y el radio de giro de la curva de flexión.
2. Esfuerzos y deformación debido a cargas externas: esfuerzos mecánicos y térmicos y Ley de Hooke
En general un esfuerzo es el resultado de la división entre una fuerza y el área en la que se aplica. Se distinguen dos direcciones para las fuerzas, las que son normales al área en la que se aplican y las que son paralelas al área en que se aplican. Si la fuerza aplicada no es normal ni paralela a la superficie, siempre puede descomponerse en la suma vectorial de otras dos que siempre resultan ser una normal y la otra paralela.
Los esfuerzos con dirección normal a la sección, se denotan como σ (sigma) y representa un esfuerzo de tracción cuando apunta hacia afuera de la sección, tratando de estirar al elemento analizado. En cambio, representa un esfuerzo de compresión cuando apunta hacia la sección, tratando de aplastar al elemento analizado.
El esfuerzo con dirección paralela al área en la que se aplica se denota como τ (tau) y representa un esfuerzo de corte. Este esfuerzo, trata de cortar el elemento analizado, tal como una tijera cuando corta papel, uno de sus filos mueven el papel hacia un lado mientras el otro filo lo mueve en dirección contraria resultando en el desgarro del papel a lo largo de una línea.
Las unidades de los esfuerzos son las mismas que para la presión, fuerza dividida por área, se utilizan con frecuencia : MPa, psia, kpsia, kg/mm2, kg/cm2.
Algunas de las propiedades mecánicas de la materia son la elasticidad, la compresión y la tensión.
Definimos a un cuerpo elástico, como aquel que recobra su tamaño y forma original cuando deja de actuar sobre él una fuerza deformante. Las bandas de hule, las pelotas de golf, los trampolines, las camas elásticas, las pelotas de fútbol y los resortes son ejemplos comunes de cuerpos elásticos. Para todos los cuerpos elásticos, conviene establecer relaciones de causa y efecto entre la deformación y las fuerzas deformantes.
Ley de Hooke
Robert Hooke fue el primero en establecer esta relación por medio de la invención de un volante para resorte para reloj. En términos generales, Hooke descubrió que cuando una fuerza F, actúa sobre un resorte, produce en él un alargamiento s que es directamente proporcional a la magnitud de la fuerza aplicada. La Ley de Hooke se representa como:
F = ks.
La constante de proporcionalidad k varía mucho de acuerdo con el tipo de material y recibe el nombre de constante del resorte. Para el ejemplo anterior, la constante del resorte es de:
k = F/s = 19.6 N/cm
La eficacia de cualquier fuerza que produce un esfuerzo depende en gran medida del área sobre la que se distribuye la fuerza, por ello una definición más completa del esfuerzo se puede enunciar de la siguiente forma:
Esfuerzo: es la razón de una fuerza aplicada entre el área sobre el cual actúa, por ejemplo Newtons/m2, o libras/ft2.
Deformación: es el cambio relativo en las dimensiones o en la forma de un cuerpo como resultado de la aplicación de un esfuerzo.
En el caso de un esfuerzo de tensión o de compresión, la deformación puede considerarse como un cambio en la longitud por unidad de longitud.
El límite elástico es el esfuerzo máximo que puede sufrir un cuerpo sin que la deformación sea permanente. Por ejemplo, un cable de aluminio cuya sección transversal es de 1 pulg2, se deforma permanentemente si se le aplica un esfuerzo de tensión mayor de 19000 libras . Esto no significa que el cable se romperá en ese punto, sino que únicamente que el cable no recuperará su tamaño original. En realidad, se puede incrementar la tensión hasta casi 21000 libras antes de que el cable se rompa. Esta propiedad de los metales les permite ser convertidos en alambres de secciones transversales más pequeñas. El mayor esfuerzo al que se puede someter un alambre sin que se rompa recibe el nombre de límite de rotura.
Si no se excede el límite elástico, de un material, podemos aplicar la Ley de Hooke a cualquier deformación elástica. Dentro de los límites para un material dado, se ha comprobado experimentalmente que la relación de un esfuerzo determinado entre la deformación que produce es una constante. En otras palabras, el esfuerzo es directamente proporcional a la deformación.
Siempre que no se exceda el límite elástico, una deformación elástica es directamente proporcional a la magnitud de la fuerza aplicada por unidad de área (esfuerzo).
Si llamamos a la constante de proporcionalidad el módulo de elasticidad, podemos escribir la Ley de Hooke en su forma más general:
Módulo de elasticidad = esfuerzo
Deformación
Los esfuerzos y deformaciones son longitudinales cuando se aplican a alambres, varillas, o barras. El esfuerzo longitudinal está dado por:
Esfuerzo longitudinal = F/A.
La unidad del esfuerzo longitudinal en el Sistema Internacional es el Newton/metro cuadrado, el cual se redefine como Pascal:
1 Pa = 1 N/m2.
En el Sistema Inglés es la libra por pulgada cuadrada:e
1 lb/in2= 6895 Pa = 6.895 kPa.
El efecto del esfuerzo de tensión es el alargamiento del alambre, o sea un incremento en su longitud. Entonces, la deformación longitudinal puede representarse mediante el cambio de longitud por unidad de longitud, podemos escribir:
Deformación longitudinal = ∆l/l
Donde l es la longitud original, ∆l es la elongación (alargamiento total). Se ha demostrado experimentalmente que hay una disminución similar en la longitud como resultado de un esfuerzo de compresión. Las mismas ecuaciones se aplican ya sea que se trate de un objeto sujeto a tensión o de un objeto a compresión.
3. Vigas con dos apoyos cargadas en puntos: vigas con cargas uniformes, vigas hiperestaticas y vigas en Cantiliver
La viga es un elemento constructivo que trabaja a flexión, cuyo esfuerzo genera tensiones de tracción y compresión. Cuando las vigas se encuentran en el perímetro exterior de un forjado, es posible que también se produzcan tensiones por torsión.
Es un elemento fundamental en la construcción, sea ésta de cualquier material. Será el tipo, calidad y fin de la construcción lo que determinará medidas, materiales de la viga y, sobre todo su capacidad de sostener y contener pesos y tensiones.
En las vigas, la longitud predomina sobre las otras dos dimensiones y suele ser horizontal. El esfuerzo de flexión provoca tensiones de tracción y compresión, produciéndose las máximas en el cordón inferior y en el cordón superior respectivamente, las cuales se calculan relacionando el momento sector y el segundo momento de inercia. En las zonas cercanas a los apoyos se producen esfuerzos cortantes o punzo amiento. También pueden producirse tensiones por torsión, sobre todo en las vigas que forman el perímetro exterior de un forjado.
Viga proviene del latín biga, un término que hacía referencia al carro de dos caballos. En la actualidad, el término se utiliza para nombrar a un hierro o madero largo y grueso, que permite sostener los techos de las construcciones o asegurarla estructura. Como bien sabemos la viga es una estructura horizontal que puede sostener cargas entre dos apoyos sin crear empuje lateral en éstos.
Generalmente son cuerpos sólidos de forma alargada y sección recta constante, de gran interés en ingeniería y arquitectura, que normalmente se utilizan en posición horizontal y siendo su longitud grande comparada con las dimensiones de su sección recta. Las vigas pueden estar sometidas a cargas concentradas, cargas distribuidas, o a pares (momentos concentrados) que actúen solos o en una combinación cualquiera, siendo la flexión la principal deformación que sufren.
El uso más imponente de una viga tal vez sea el que aplica a la estructura de puentes y su diseño de ingeniería descansa justamente sobre vigas de calidades y tamaños acordes al tipo y uso de puente que se desea construir. Esta estructura desarrolla compresión en la parte de arriba y tensión en la de abajo. Pensemos que los primeros puentes de la humanidad fueron construidos con vigas de madera: primitivos troncos o vigas que unían dos orillas.
Problemas de esfuerzos longitudinales.
1.- Un alambre de teléfono de 120 m de largo, y 2.2. mm de diámetro se estira debido a una fuerza de 380 N. ¿Cuál es el esfuerzo longitudinal? Si la longitud después de ser estirado es de 120.10 m . ¿Cuál es la deformación longitudinal?. Determine el módulo de Young para el alambre?.
Solución: El área de la sección transversal del alambre es de
A = π D2 = (3.14) (2.2 x 10-3 m)2 = 3.8 x 10-6 m2.
4 4
Esfuerzo = F/A = 380 N = 100 x 106N/m2. = 100 MPa.
3.8 x 10-6 m2.
Deformación = ∆l/l = 0.10 m/120 m = 8.3 x 10-4.
Y = esfuerzo/deformación = 100 MPa/8.3 x 10-4. = 120000 MPa.
2.- ¿Cuál es la máxima carga que se puede colgar de un alambre de acero de 6 mm de diámetro sin exceder su límite elástico?. Determine el incremento en la longitud bajo el efecto de esta carga, si la longitud original es de 2 metros.
Solución: a partir de la tabla anterior, el límite elástico para el acero es de 248 Mpa o 2.48 x 108 Pa. Puesto que este valor representa el esfuerzo limitante, escribimos:
F/A = 2.48 x 108 Pa
Donde A es el área obtenida a partir de:
A = π D2 = (3.14) (0.006 m)2 = 2.83 x 10-5m2.
4 4
Por lo tanto, la carga limitadora F es el esfuerzo limitador multiplicado por el área:
F = (2.48 x 108 Pa) (2.83 x 10-5 m2.) = 7.01 x 103 N.
La mayor masa que puede soportarse se calcula a partir de este peso:
m = P/g m = 7.01 x 103 kg m/seg2. = 716 kg.
9.8 m/seg2.
El incremento de la longitud bajo dicha carga se encuentra a partir de la ecuación:
∆l = 1 (F/A) = 2 m (2.48 x 108 Pa) = 2.40 x 10-3 m.
Y 2.07 x 1011 Pa
La longitud aumenta en 2.40 mm y la nueva longitud es de 2.0024 m.
4. Clasificación de columnas
Las columnas son elementos que sostienen: principalmente cargas a compresión en general las columnas también soportan momentos flectores (o de flexión) Con respecto a uno o a los dos ejes de la sección transversal y esta acción puede producir fuerzas de tención sobre una parte de la sección transversal sirven para apoyar las vigas cargadas y estas transmiten la carga de los pisos superiores hasta la planta baja y después al suelo.
Las columnas se suelen dividir en dos grupos: largas e intermedias.
En algunos casos, los elementos cortos sometidos a compresión se consideran en un tercer grupo Columnas largas, Columnas de longitud intermedia, Columnas con carga excéntrica, Columnas cortas con carga excéntrica, Columnas con varios tipos de soporte. Aunque pueden recibir otros nombres, como se muestra en la siguiente ilustración.
Para analizar la capacidad de carga de las columnas se deben referir al conjunto al que pertenecen y al sistema en el que trabajan; es decir, a las características generales.
Carga crítica en columnas articuladas.
Consideremos una viga articulada en sus extremos mediante rótulas que permiten la flexión en todas las direcciones, tal como se muestra en la figura. Si aplicamos una fuerza horizontal “H” en un punto medio de la viga se producirá una deflexión.
Columnas largas, cortas e intermedias.
Mediante ensayos mecánicos realizados en columnas se ha demostrado que la carga crítica señalada por las ecuaciones de Euler y de la secante puede ser superior a la carga crítica real necesaria para pandea r la columna, como muestra el gráfico.
Columnas Cortas. A este grupo pertenecen elementos cargados axialmente a compresión con relaciones de esbeltez muy pequeñas, en los que no se produce pandeo y la falla ocurre cuando ‘ Max ≈ y’.
Columnas Intermedias. Cuando en los elementos cargados comienza a presentarse el fenómeno de pandeo al éstos experimentar esfuerzos menores a “ y”. La ecuación de Euler no se aproxima satisfactoriamente al comportamiento de la columna, requiriendo esta zona de ecuaciones experimentales complejas para predecir con cierta precisión el valor del esfuerzo crítico (con el cual comienza el pandeo en la columna).
Columnas Largas. Referida a aquellos elementos con grandes relaciones de esbeltez. La ecuación de Euler describe con precisión aceptable el comportamiento de estas columnas.
5. Conclusiones y créditos
Este trabajo se realizó para la clase de física impartida por el ingeniero José Alfredo Solorio Leyva.
Participantes
Conceptos:
"En conclusión, conocer los conceptos básicos del tema, nos sirve para entender y resolver alguna duda de lo que vallamos conociendo durante el tema así como también conocer los conceptos antes de iniciar el tema nos puede ayudar a tener una mejor visión del tema como una idea más clara de los que se trata esta unidad y como consecuencia un mejor aprendizaje"
- Cervantes Silva Alejandro
Esfuerzo y deformación
"Los esfuerzos en los materiales pueden influir mucho sobre como se trabajará algún maquinado o simplemente la forma en como se trabaja con ellos, nos da a demostrar que la física interviene mucho y por ello es importante conocerla junto a sus cálculos, esto para evitar fallos cuando se trate de algún proceso de fabricación con los materiales. Y no solo se vería en eso, si no también en nuestro día a día con cosas tan simples como levantar una cosa del suelo, solo que obviamente se ve menos complejo"
- Cobian López Cielo Dannae
Vigas
" Este tipo de vigas se usan normalmente en las edificaciones porque tienen la ventaja de que no vibran por la acción de la carga para la que están diseñadas, aunque se corre el riesgo de que al ocurrir un sismo la fuerza de este sobrepase la resistencia de su diseño y rompa la estructura pero para que pase esto tiene que ser un sismo muy fuerte."
- Gonzáles Andrade Joseph Kevin
Columnas
"Las columnas son soportes verticales que se encargan de resistir a la compresión por medio de cargas acumuladas sobre ellas, existen 3 principales categorías de columnas, las cuales son largas, cortas e intermedias. Su principal distintivo es la longitud que varía entre sí. Cada tipo de columna presenta un comportamiento diferente de “oposición a la carga” como lo puede ser la contracción de la estructura que conforma a la columna y así consigue una transformación por deformación debido a las fuerzas aplicadas. Como se había mostrado gráficamente, existen maneras de determinar los esfuerzos y deformaciones para las columnas, comprenden de un comportamiento referido a ensayos destructivos y no destructivos, al aplicar fuerzas de compresión, el material o bien la columna sufre deformaciones por reacción a los aplastamientos que debilitan y fracturan el componente"
- Graneros Hernández Julio César
6. Bibliografía
Conceptos
https://es.slideshare.net/franklingualaquiza/conceptos-basicos-de-resistencia-de-materiales-para-rendir-un-examenen
https://es.khanacademy.org/science/physics/forces-newtons-laws/tension-tutorial/a/what-is-tension
https://es.slideshare.net/ezetabrajanramirez/41-esfuerzo-y-deformacin-debido-a-cargas-externas
https://kupdf.net/queue/vigas-con-dos-apoyos-cargadas-en-puntos_5be78d3ae2b6f57f2102404e_pdf?queue_id=-1&x=1590477284&z=MTc3LjI0NC4xNzIuMjA5
https://prezi.com/htes9kncrkxd/42-vigas-con-dos-apoyos-cargadas-en-puntos-vigas-con-carga/
https://vdocuments.mx/download/vigas-con-dos-apoyos-cargadas-en-puntos
https://prezi.com/pjbpbfkrdytw/43-clasificacion-de-columnas/
Esfuerzos
http://fisicaingenieriaindustrial.blogspot.com/2016/04/link-para-imprimir-unidad-iv.html?m=1
Vigas
http://www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r81669.PDF
https://www.academia.edu
https://www.google.com/urlsa=t&source=web&rct=j&url=
http://fisicaingenieriaindustrial.blogspot.com/2016/04/link-para-imprimir-unidad-iv.html%3Fm%3D1&ved=2ahUKEwiO2e_75NTpAhWvHDQIHQNNAyMQFjAEegQIAhAB&usg=AOvVaw1lVROQxhTnx5tnf0Ju3Nem
Columnas
https://es.scribd.com/document/362323069/clasificacion-de-columnas-docx
https://www.ecured.cu/Columnas
http://www.ula.ve/facultad-ingenieria/images/mecanica/Mecanica_Materiales/I/Tema6.pdf
https://prezi.com/bnjtwvix3kpw/formula-de-euler-y-de-johnson-para-columnas/
https://studylib.es/doc/5293225/columnas
Mayo, 2020
Comentarios
Publicar un comentario